The quantum mechanics of cricket

A must read for all cricket lovers with science background :-).
A good article from Joe Wolfe (School of Physics, University of New South Wales)

The diagram at below shows how a batsman leaves a parallel slit (width a = 180 mm) between bat and pad, through which a cricket ball with momentum p can diffract. On 23 October, 1999, Australian captain Steve ('Tugga') Waugh, perhaps b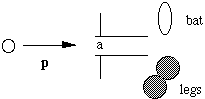ecause of his intuitive knowledge of quantum mechanics, appears to have set the field at maxima in |Y²|, where Y is the wave function of the cricket ball, as is shown in the photograph below. Showing all reasoning and calculation, determine

1) whom he should ask to bowl, and

2) howzat?

We also answer one classical question about cricket ball motion.

The small angle approximation is a bit crude for the angular spacing Dq, but will suffice for this approximate analysis, so

Dq ~ l.Da/pa,

where Da is the spacing between maxima of |Y²|. Inspection of the graph above shows that, except for the wicket keeper, this spacing is approximately the same as the spacing of the subsidiary minima in |Y²|, which requires a phase difference of p. So

Dq ~ l/a,

where l is the wavelength of the cricket ball. This is given by the de Broglie equation l = h/p, where h is Planck's constant. With the exception of some anecdotal claims concerning Jeff Thomson, who retired before the introduction of regular bowling speed measurements, the speed is non-relativistic, so p = mv is a good approximation. Substitution gives

Dq ~ h/amv, so:
v ~ h/amDq = hL/amDy

Substitution gives a speed of 3 x 10^-30 ms^-1. This is rather slow: indeed it is less than one atomic radius per age of the universe. So, to answer question (1): We strongly suspect that no-one can bowl this slowly at ordinary temperatures, but if one is looking for improbable feats from a slow bowler, it is likely to be Shane Warne.

We return now to question (2) about the fate of the batsman. Is he

a) out caught
b) out lbw
c) out interfering with ball?

In fact, given that the sun will have gone out (not down, but out) in the 2 x 10²⁴ years that the ball takes to reach him, we expect that an appeal against the light will be successful.

For cricket lovers: the bowler was Damien Flemming. The batsman was David Mutandera of Zimbabwe. This is believed to be the first time in cricket history such a field has been employed in an international one day match. Zimbabwe were all out for 116 runs in the second one day international at the Harare Sports Club, 23 October 1999.

---

Just in case: Newtonian mechanics (including the fluid mechanics of the air) is completely adequate to describe the behaviour of cricket balls, although the existence, stability and chemical properties of the atoms and molecules of which they are made are all determined by quantum mechanics. So yes, the whole page above is a joke, whose original purpose was both to amuse first year physics students and to demonstrate the very small size of quantum mechanical effects in the familiar, macroscopic world. The Brownian motion of the cricket ball (its irregular, random motion due to its collisions with molecules of air) is typically ten billion times greater than the velocity calculated above. The disturbance of quantum mechanical effects such as particle interference by random thermal motion is why even nano-scale quantum effects are often studied at low temperatures.

A classical question: When does the cricket ball travel its fastest (towards the batsman)?

This question was asked by Dan Trouw of Darwin. Let's answer it using classical mechanics, rather than quantum mechanics, while recognising that quantum mechanics reduces to the classical result in typical macroscopic circumstances, such as cricket.

The question is an interesting one: the ball is released above ground level, so it has a couple of metres to fall. On the other hand, air resistance is slowing it from the moment it leaves the hand. Which force 'wins'? The answer is not immediately obvious -- to me, at least. On the one hand, the trajectory of a well-hit is obviously not a parabola: it falls more rapidly than one would expect. So the force of air resistance is obviously considerable. On the other, a ball dropped from rest would take a long time to approach terminal velocity. So a calculation is necessary.

The force of gravity is easy, it's the weight, W = mg. Let's compare it with the force F_drag due to turbulent drag. This is given by:
F_drag = (1/2)C_DAρv²,
where v is the speed, ρ is the density of air, A is the cross-sectional area, and C_D is the drag coefficient. This coefficient, which is around unity for very blunt objects and which decreases for streamlined objects, must be measured experimentally, For a sphere it is typically about 0.5. So we have
F_drag ≈ 0.25πv²ρv²,
The density of air is about 1.2 kg.m^-3. So, for a very fast bowler, with v = 40 m/s, this force is about 2 newtons: for such a bowler, the drag force is about the same as the weight of the cricket ball. For someone bowling at say 20 m/s, the drag force would be only a few tenths of the weight.

Thus, for a ball bowled vertically downwards (a new meaning for shooting one's self in the foot), and for a slow bowler, weight would be more important than drag, as it clearly is when the ball is dropped.

However, the ball is not bowled vertically down -- at least not deliberately. It is easiest to include the effect of direction by considering kinetic energy. The work done by a force is the magnitude of the force times the component of displacement in the direction of the force. Gravity has only about two metres of downwards vertical travel over which to accelerate the ball, while the drag has about twelve metres (more for a slow bowler) to decelerate it. And a very slow bowler would have to bowl the ball slightly upwards ("give it a bit of air") just so that it covers the distance. In which case, gravity would act to slow it at first, not accelerate it.

Consequently, drag has a greater effect on reducing the kinetic energy (and thus slowing it) than has gravity in increasing it. So, even for quite slow bowlers, the fastest that the ball is travelling is just when it leaves the bowler's hand -- until, of course, it reaches the bat.